Решение систем линейных уравнений, примеры здесь.
- Системы m линейных уравнений с n неизвестными.
Решение системы линейных уравнений — это такое множество чисел {x1, x2, …, xn}, при подстановке которых в каждое из уравнений системы получается верное равенство.
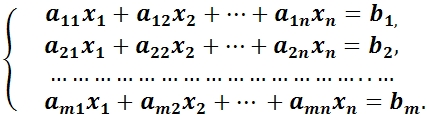 где aij, i = 1, …, m; j = 1, …, n — коэффициенты системы;
где aij, i = 1, …, m; j = 1, …, n — коэффициенты системы;
bi, i = 1, …, m — свободные члены;
xj, j = 1, …, n — неизвестные.
Вышеприведенная система может быть записана в матричном виде: A · X = B,

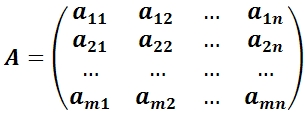
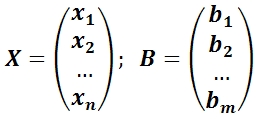
где (A|B) — основная матрица системы;
A — расширенная матрица системы;
X — столбец неизвестных;
B — столбец свободных членов.
Если матрица B не является нуль-матрицей ∅, то данная система линейных уравнений называется неоднородной.
Если матрица B = ∅, то данная система линейных уравнений называется однородной. Однородная система всегда имеет нулевое (тривиальное) решение: x1 = x2 = …, xn = 0.
Совместная система линейных уравнений — это имеющая решение система линейных уравнений.
Несовместная система линейных уравнений — это не имеющая решение система линейных уравнений.
Определённая система линейных уравнений — это имеющая единственное решение система линейных уравнений.
Неопределённая система линейных уравнений — это имеющая бесконечное множество решений система линейных уравнений. - Системы n линейных уравнений с n неизвестными
Если число неизвестных равно числу уравнений, то матрица – квадратная. Определитель матрицы называется главным определителем системы линейных уравнений и обозначается символом Δ.
Метод Крамера для решения систем n линейных уравнений с n неизвестными.
Правило Крамера.
Если главный определитель системы линейных уравнений не равен нулю, то система совместна и определена, причем единственное решение вычисляется по формулам Крамера:
где Δi — определители, получаемые из главного определителя системы Δ заменой i-го столбца на столбец свободных членов. Пример 9. - Системы m линейных уравнений с n неизвестными
Теорема Кронекера−Капелли.

Для того чтобы данная система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы системы, rang(Α) = rang(Α|B).
Если rang(Α) ≠ rang(Α|B), то система заведомо не имеет решений.
Eсли rang(Α) = rang(Α|B), то возможны два случая:
1) rang(Α) = n (числу неизвестных) − решение единственно и может быть получено по формулам Крамера;
2) rang(Α) < n − решений бесконечно много. - Метод Гаусса для решения систем линейных уравнений

Составим расширенную матрицу (A|B) данной системы из коэффициентов при неизвестных и правых частей.
Метод Гаусса или метод исключения неизвестных состоит в приведении расширенной матрицы (A|B) с помощью элементарных преобразований над ее строками к диагональному виду (к верхнему треугольному виду). Возвращаясь к системе уравнений, определяют все неизвестные.
К элементарным преобразованиям над строками относятся следующие:
1) перемена местами двух строк;
2) умножение строки на число, отличное от 0;
3) прибавление к строке другой строки, умноженной на произвольное число;
4) выбрасывание нулевой строки.
Расширенной матрице, приведенной к диагональному виду, соответствует линейная система, эквивалентная данной, решение которой не вызывает затруднений. Пример 10. - Система однородных линейных уравнений.
Однородная система имеет вид:

ей соответствует матричное уравнение A · X = 0.
1) Однородная система всегда совместна, так как r(A) = r(A|B), всегда существует нулевое решение (0, 0, …, 0).
2) Для того чтобы однородная система имела ненулевое решение, необходимо и достаточно, чтобы r = r(A) < n, что равносильно Δ = 0.
3) Если r < n, то заведомо Δ = 0, тогда возникают свободные неизвестные c1, c2, …, cn-r, система имеет нетривиальные решения, причем их бесконечно много.
4) Общее решение X при r < n может быть записано в матричном виде следующим образом:
X = c1 · X1 + c2 · X2 + … + cn-r · Xn-r,
где решения X1, X2, …, Xn-r образуют фундаментальную систему решений.
5) Фундаментальная система решений может быть получена из общего решения однородной системы:
 ,
,
если последовательно полагать значения параметров равными (1, 0, …, 0), (0, 1, …, 0), …, (0, 0, …,1).
Разложение общего решения по фундаментальной системе решений — это запись общего решения в виде линейной комбинации решений, принадлежащих к фундаментальной системе.
Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.
Итак, если определитель Δ ≠ 0, то система имеет единственное решение.
Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.
Теорема. Для того чтобы однородная система имела ненулевое решение, необходимо и достаточно, чтобы r(A) < n.
Доказательство:
1) r не может быть больше n (ранг матрицы не превышает числа столбцов или строк);
2) r < n, т.к. если r = n, то главный определитель системы Δ ≠ 0, и, по формулам Крамера, существует единственное тривиальное решение x1 = x2 = … = xn = 0, что противоречит условию. Значит, r(A) < n.
Следствие. Для того чтобы однородная система n линейных уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы Δ = 0.