Виды матриц.
- Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах

где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
Сокращённое обозначение матрицы A=(aij)m×n.
- Порядок матрицы — это число ее строк или столбцов.
- Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
- Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
- Квадратная матрица — это матрица у которой число строк равно числу столбцов:
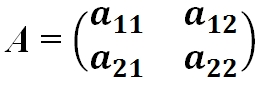
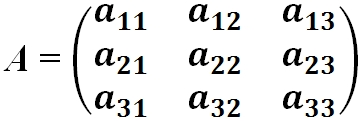
- Матрица-столбец — это матрица, у которой всего один столбец:
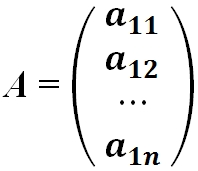
- Матрица-строка — это матрица, у которой всего одна строка:
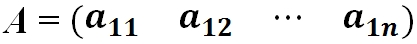
- Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
- Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
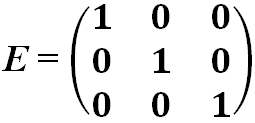
- Матрица квадратная диагональная:
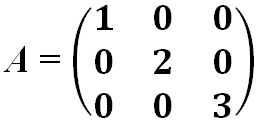
- Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
- Матрица верхняя треугольная:
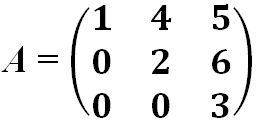
- Матрица нижняя треугольная:
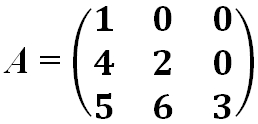
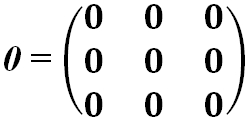
- Нулевая матрица — это матрица, все элементы которой равны 0:
Операции над матрицами.
- Равенство матриц.
Две матрицы A (aij), B (bij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
то есть при всех i, j aij=bij.
- Сложение матриц.
Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1.
- Умножение матрицы на число.
Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2.
- Умножение матриц.
Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
cij=ai1b1j+ai2b2j+ … aikbkj.
Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3.
- Транспонированные матрицы.
Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
Полученная матрица обозначается через A' или AT. Пример 4.
Квадратная матрица называется симметричной, если A=A', то есть для элементов выполнены равенства aij=aji.
- Обратная матрица.
Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:

Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная  , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1) 
2) 
3) 
4) 
- Алгоритм нахождения А-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим Mij — все миноры матрицы A.
3) Определяем 
4) Строим матрицу алгебраических дополнений  и транспонируем:
и транспонируем: 
5) Делим каждый элемент матрицы на det A:  Пример 5.
Пример 5.
- Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число.
- Решение матричных уравнений.
Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
Простейшие типы матричных уравнений:
1)  . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,
|A| ≠ 0, следовательно, существует обратная матрица A-1.
Умножим уравнение на A-1 слева: 
2)  . Матрица A – квадратная, |A| ≠ 0.
. Матрица A – квадратная, |A| ≠ 0.
Умножим уравнение на A-1 справа:  .
.
3)  . Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
Умножим уравнение на A-1 слева: 
Умножим уравнение на B-1 справа:  .
.
- Ранг матрицы.
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
Mk этой матрицы: 
Матрицы называются эквивалентными, что обозначается
A ∼ B, если  .
.
Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.
- Метод окаймляющих миноров.
Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка:  .
.
Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6.
- Метод элементарных преобразований.
Элементарные преобразования матрицы не меняют ее ранга.
К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
Для определения ранга матрицы A методом элементарных преобразований следует:
1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
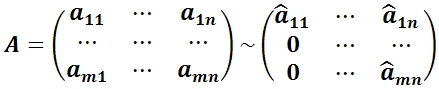
3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
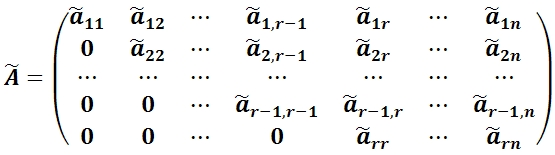
Тогда ранг матрицы A равен: rang A = rang Ã.
Определитель матрицы.
- Определитель квадратной матрицы.
Определитель первого порядка представляет собой число.
Определитель квадратной матрицы порядка n A=(aij)m×n обозначается символами: 
Определитель квадратной матрицы A второго порядка — это число, равное: 
Определитель квадратной матрицы А третьего порядка — это число, равное:

 . Пример 7.
. Пример 7.
- Правило треугольников (правило Саррюса):
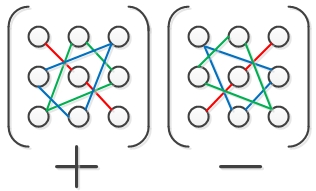
Знаки (+) и (–) соответствуют знакам определенных слагаемых, входящих в определитель, элементы определителя изображаются кружками, а соответствующие произведения — отрезками или треугольниками.
- Алгебраическое дополнение A=(aij) элемента aij — это определитель n-1 порядка, полученный из |A| вычеркиванием i-й строки и j-го столбца, на пересечении которых стоит элемент aij, взятый со знаком (-1)i+j.
Свойства определителей.
- Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
- При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:

- Определитель, содержащий две одинаковые строки (столбца), равен нулю.
- Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:

- Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):

- Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
- Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:


- Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:

- Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:

- Определитель произведения матриц А и В равен произведению их определителей:
 .
.
Определители n–го порядка.
- Минор Мij или Δij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент aij.
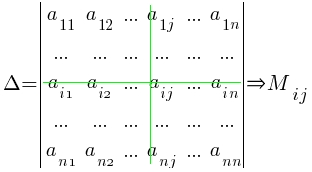
- Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
Для определителей n-го порядка имеют место все перечисленные выше свойства определителей.
- Правило выбора знака перед минором в алгебраическом дополнении:

- Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
- Метод сведения к треугольному виду.
Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.
Формулы, уравнения, теоремы, примеры решения задач

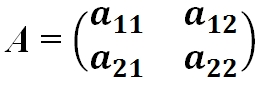
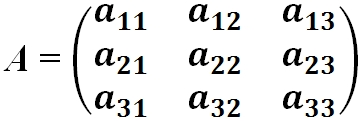
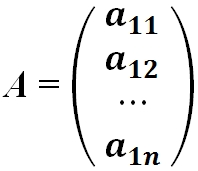
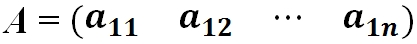
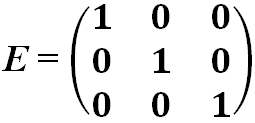
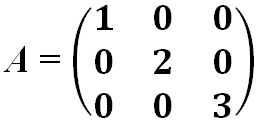
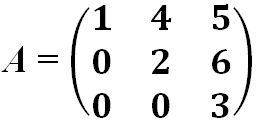
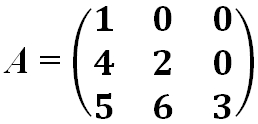


 , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).




 и транспонируем:
и транспонируем: 
 Пример 5.
Пример 5. . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,
 . Матрица A – квадратная, |A| ≠ 0.
. Матрица A – квадратная, |A| ≠ 0. .
. . Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
 .
.
 .
. .
.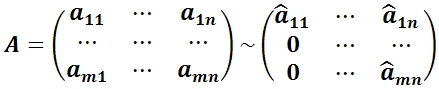
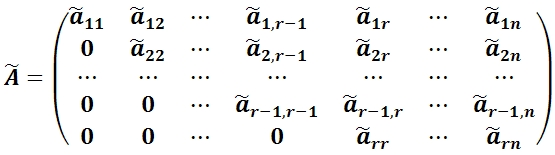



 . Пример 7.
. Пример 7.








 .
.
