Примеры решения задач

Примеры решения задач по высшей математике

Задачи по математике, решенные примеры здесь.

Матрицы и определители

Пример 1. Сумма матриц

Дано:
Матрицы A и B.
A=(matrix{2}{3}{1 2 {3~} 4 5 {6~}}) , B=(matrix{2}{3}{6 5 {4~} 3 2 {1~}})
Найти:
Сумму матриц A + B = C.
C- ?

Решение:
Для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах.
Таким образом, суммой двух матриц A и B является матрица:

C=A+B=(matrix{2}{3}{1 2 {3~} 4 5 {6~}})+(matrix{2}{3}{6 5 {4~} 3 2 {1~}})=(matrix{2}{3}{7 7 {7~} 7 7 {7~}})

Ответ: C=(matrix{2}{3}{7 7 {7~} 7 7 {7~}})

Пример 2. Умножение матрицы на число

Дано:
Матрица A=(matrix{2}{3}{1 2 {3~} 4 5 {6~}})
Число k=2.

Найти:
Произведение матрицы на число: A × k = B
B — ?

Решение:
Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число.
Таким образом, произведение матрицы A на число k есть новая матрица:

B=2*A=2*(matrix{2}{3}{1 2 {3~} 4 5 {6~}})=(matrix{2}{3}{2 4 {6~} 8 10 {12~}})

Ответ: B=(matrix{2}{3}{2 4 {6~} 8 10 {12~}})

Пример 3. Умножение матриц

Дано:
Матрица A=(matrix{2}{3}{2 3 {1~} {-1} 0 {1~}}) ;
Матрица B=(matrix{3}{2}{2 {1~} {-1} {1~} 3 {-2~}}) .

Найти:
Произведение матриц: A × B = C
C — ?

Решение:
Каждый элемент матрицы С = A × B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Строки матрицы А умножаем на столбцы матрицы В и получаем:

C=A*B=(matrix{2}{3}{2 3 {1~} {-1} 0 {1~}})*(matrix{3}{2}{2 {1~} {-1} {1~} 3 {-2~}})=

{}=(matrix{2}{2}{{2*2+3*(-1)+1*3} {2*1+3*1+1*(-2)} {-1*2+0*(-1)+1*3} {-1*1+0*1+1*(-2)}})

C=A*B=(matrix{2}{2}{4 {3~} 1 {-3~}})

Ответ: C=(matrix{2}{2}{4 {3~} 1 {-3~}})

Пример 4. Транспонирование матрицы

Дано:
Матрица A=(matrix{2}{3}{7 8 {9~} 1 2 {3~}}) .

Найти:
Найти матрицу транспонированную данной.
A^T — ?

Решение:
Транспонирование матрицы А заключается в замене строк этой матрицы ее столбцами с сохранением их номеров. Полученная матрица обозначается через A^T

$A=(matrix{2}{3}{7 8 {9~} 1 2 {3~}}) {doubleright} A^T=(matrix{3}{2}{7 {1~} 8 {2~} 9 {3~}})$

Ответ: $A^T=(matrix{3}{2}{7 {1~} 8 {2~} 9 {3~}})$

Пример 5. Обратная матрица

Дано:
Матрица A=(matrix{2}{2}{2 {-1~} 3 {1~}}) .

Найти:
Найти обратную матрицу для матрицы A.
A^-1 — ?

Решение:
Находим det A и проверяем det A ≠ 0:
{det A}=delim{|}{matrix{2}{2}{ 2 {-1} 3 1 }}{|}=2*1-3*(-1)=5 . det A = 5 ≠ 0.

Составляем вспомогательную матрицу A^V из алгебраических дополнений A_ij: ${A^V}=(matrix{2}{2}{1 {-3~} 1 {2~}})$ .

Транспонируем матрицу A^V:
$(A^V)^T=(matrix{2}{2}{1 {1~} {-3} {2~}})$ .

Каждый элемент, полученной матрицы, делим на на det A:
$A^{-1}={1/{det A}}(A^V)^T={1/5}*(matrix{2}{2}{1 {1~} {-3} {2~}})=(matrix{2}{2}{{1/5} {1/5} {-3/5} {2/5}})$

Ответ: $A^{-1}=(matrix{2}{2}{{1/5} {1/5} {-3/5} {2/5}})$

Пример 6. Ранг матрицы

Дано:
Матрица A=(matrix{3}{3}{1 {-1} {1~} 2 {-2} {2~} 1 1 {-1~}}) .

Найти:
Ранг матрицы A.
r(A) — ?

Решение:
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров M_k этой матрицы. Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований.

Вычислим ранг матрицы, применив метод окаймляющих миноров.
$M_1=1;~{M^1}_2=delim{|}{matrix{2}{2}{1 {-1~} 2 {-2~}}}{|}=-1*2-2*(-1)=0;$

${M^2}_2=delim{|}{matrix{2}{2}{{-1} {1~} {-2} {2~}}}{|}=-1*2-(-2)*1=0;~{M^3}_2=delim{|}{matrix{2}{2}{2 {-2~} 1 {1~}}}{|}=2*1-1*(-2)=4;$

M³₂≠0; $M_3=delim{|}{matrix{3}{3}{1 {-1} {1~} 2 {-2} {2~} 1 1 {-1~}}}{|}=1*(-2)*(-1)+(-1)*2*1+1*2*(-1)-$

{}-1*(-2)*1-(-1)*2*(-1)-1*2*(-1)=0~{doubleright}~r(A)=2 .

Ответ: r(A) = 2

Пример 7. Определитель квадратной матрицы

Дано:
Матрица A=(matrix{3}{3}{3 {-1} {-1~} {-3} 1 {5~} 2 {-2} {4~}}) .

Найти:
Определитель |A| матрицы A.
|A| — ?

Решение:
Каждой квадратной матрице А можно поставить в соответствие число, которое называется ее определителем и обозначается det А или |А|. Определитель матрицы третьего порядка вычисляется через ее элементы, по следующей формуле:
$det A = delim{|}{A}{|} = delim{|}{matrix{3}{3}{{a_{11}} {a_{12}} {a_{13}} {a_{21}} {a_{22}} {a_{23}} {a_{31}} {a_{32}} {a_{33}}} }{|} = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} +$
${}+ a_{13}a_{21}a_{32} - a_{13}a_{22}a_{31} - a_{12}a_{21}a_{33} - a_{11}a_{23}a_{32}$
Тогда, для данной в примере матрицы A, определитель |A| будет равен:
delim{|}{A}{|}=delim{|}{matrix{3}{3}{ 3 {-1} {-1} {-3} 1 5 2 {-2} 4 } }{|}=3*1*4+(-1)*5*2+(-1)*(-3)*(-2)-
{}-2*1*(-1)-(-1)*(-3)*4-3*5*(-2)=16

Ответ: |A| = 16.

Пример 8. Минор и алгебраическое дополнение

Дано:
Матрица A=(matrix{3}{3}{3 {-1} {-1~} {-3} 1 {5~} 2 {-2} {4~}}) .

Найти:
Минор и алгебраическое дополнение элемента a₂₁ определителя |A| матрицы A.
Δ₂₁ — ? A₂₁ — ?

Решение:
Запишем определитель матрицы A: delim{|}A{|}=delim{|}{matrix{3}{3}{3 {-1} {-1~} {-3} 1 {5~} 2 {-2} {4~}}}{|} .

Минор элемента a₂₁ определителя |A|- это определитель, который получится из данного вычеркиванием 2-й строки и 1-го столбца. Для минора используют обозначение Δ₂₁.
${Delta}_{21}=delim{|}{matrix{2}{2}{{-1} {-1~} {-2} {4~}}}{|}=-1*4-(-2*(-1))=-6$

Алгебраическое дополнение A₂₁ элемента a₂₁ в определителе — это число, которое вычисляется по правилу: A_ij = (-1)^i+j · Δ_ij, где Δ_ij — соответствующий минор. Тогда, подставив данные в формулу, получим:
A₂₁ = (-1)²⁺¹ · (-6) = 6.

Ответ: Δ₂₁ = -6; A₂₁ = 6.

Системы линейных уравнений

Пример 9. Метод Крамера

Дано:
Система линейных уравнений
$delim{lbrace}{matrix{3}{7}{{2x_1} {+} {3x_2} {+} {2x_3} {=} {9,~} {x_1} {+} {2x_2} {+} {3x_3} {=} {14,~} {3x_1} {+} {4x_2} {+} {2x_3} {=} {16.~}}}{}$

Найти:
Решение системы линейных уравнений методом Крамера.
x₁, x₂, x₃— ?

Решение:
Составляем матрицу A из коэффициентов данной системы уравнений — основную матрицу системы:
A=(matrix{3}{3}{{2} {3} {2~} {1} {2} {3~} {3} {4} {2~}})

Составляем матрицу B из свободных членов данной системы уравнений — матрицу-столбец свободных членов: B=(matrix{3}{1}{{9~} {14~} {16~}})

Решаем пример методом Крамера, используя формулы Крамера.

Вычисляем определитель (подробный пример расчета определителя) матрицы A — Δ — главный определитель системы:
{Delta}=delim{|}{matrix{3}{3}{{2} {3} {2~} {1} {2} {3~} {3} {4} {2~}}}{|}=1

Условие Δ ≠ 0 выполняется, значит система совместна и определена, причём единственное решение вычисляется по формулам Крамера:
$x_1={{Delta}_1}/{Delta},~x_2={{Delta}_2}/{Delta},~x_3={{Delta}_3}/{Delta}$

Δ₁ — 1-й вспомогательный определитель системы, получается из Δ заменой 1-го столбца на столбец свободных членов:
${Delta}_1=delim{|}{matrix{3}{3}{{9} {3} {2~} {14} {2} {3~} {16} {4} {2~}}}{|}=36$

Δ₂ — 2-й вспомогательный определитель системы, получается из Δ заменой 2-го столбца на столбец свободных членов:
${Delta}_2=delim{|}{matrix{3}{3}{{2} {9} {2~} {1} {14} {3~} {3} {16} {2~}}}{|}=-29$

Δ₃ — 3-й вспомогательный определитель системы, получается из Δ заменой 3-го столбца на столбец свободных членов:
${Delta}_3=delim{|}{matrix{3}{3}{{2} {3} {9~} {1} {2} {14~} {3} {4} {16~}}}{|}=12$

Подставив полученные значения в формулы Крамера, находим неизвестные члены уравнения:
$x_1={{Delta}_1}/{Delta}={36}/{1}=36,~x_2={{Delta}_2}/{Delta}={-29}/{1}=-29,~x_3={{Delta}_3}/{Delta}={12}/{1}=12$

Ответ: x_1=36;~x_2=-29;~x_3=12 .

Пример 10. Метод Гаусса

Дано:
Система линейных уравнений
$delim{lbrace}{matrix{3}{7}{{x_1} {+} {x_2} {+} {x_3} {=} {9,~} {4x_1} {-} {3x_2} {+} {x_3} {=} {1,~} {2x_1} {+} {x_2} {-} {x_3} {=} {1.~}}}{}$

Найти:
Решение системы линейных уравнений методом Гаусса.
x₁, x₂, x₃— ?

Решение:
Составляем расширенную матрицу (A|B) системы из коэффициентов при неизвестных и правых частей:
(A|B)= (matrix{3}{5}{{1} {1} {1} {vert} {9~} {4} {-3} {1} {vert} {1~} {2} {1} {-1} {vert} {1~}})

Приведём расширенную матрицу (A|B) системы к ступенчатому виду.

Из второй строки вычитаем первую строку, умноженную на четыре:
(A|B)~ (matrix{3}{5}{{1} {1} {1} {vert} {9~} {0} {-7} {-3} {vert} {-35~} {2} {1} {-1} {vert} {1~}})

Из третьей строки вычитаем первую строку, умноженную на два:
(A|B)~ (matrix{3}{5}{{1} {1} {1} {vert} {9~} {0} {-7} {-3} {vert} {-35~} {0} {-1} {-3} {vert} {-17~}})

Из третьей строки вычитаем вторую строку, умноженную на 1/7 :
(A|B)~ (matrix{3}{5}{{1} {1} {1} {vert} {9~} {0} {-7} {-3} {vert} {-35~} {0} {0} {-18/7} {vert} {-12~}})

Полученной диагональной матрице соответствует эквивалентная система:
$delim{lbrace}{matrix{3}{7}{{x_1} {+} {x_2} {+} {x_3} {=} {9,~} {~} {~} {-7x_2} {-} {3x_3} {=} {-35,~} {~} {~} {~} {~} {(-18/7)x_3} {=} {-12,~}}}{}{doubleright}$ $delim{lbrace}{matrix{3}{3}{{x_1} {=} {4/3,~} {x_2} {=} {3,~} {x_3} {=} {14/3.~}}}{}$

Ответ: x_1=4/3;~x_2=3;~x_3=14/3 .

Векторная алгебра

Пример 11. Координаты вектора

Дано:
Точки: A(2, -4, 0); B(-4, 6, -2).

Найти:
Координаты вектора overline{a}
— ?

Решение:
Начало вектора overline{a} совпадает с точкой А, конец – с точкой В. Находим координаты вектора :
$a_x={x_B}-{x_A}=-4-2=-6,$
$a_y={y_B}-{y_A}=6-(-4)=10,$
$a_z={z_B}-{z_A}=-2-0=-2.$

Ответ: overline{a}=delim{lbrace}{-6,~10,~-2}{rbrace}

Пример 12. Направляющие косинусы вектора

Дано:
Вектор: overline{a}=delim{lbrace}{-6,~10,~-2}{rbrace} .

Найти:
Направляющие косинусы вектора overline{a} .
cos{alpha},~cos{beta},~cos{gamma} — ?

Решение:
Координаты вектора связаны с его направляющими косинусами следующим образом:
$cos{alpha}={a_x}/{{delim{|}{a}{|}}}=-6/{sqrt{140}};$
$cos{beta}={a_y}/{{delim{|}{a}{|}}}=10/{sqrt{140}};$
$cos{gamma}={a_z}/{{delim{|}{a}{|}}}=-2/{sqrt{140}}.$

Ответ: cos{alpha}=-6/{sqrt{140}};~cos{beta}=10/{sqrt{140}};~cos{gamma}=-2/{sqrt{140}}.

Пример 13. Длина вектора

Дано:
Вектор: overline{a}=delim{lbrace}{-6,~10,~-2}{rbrace} .

Найти:
Длину вектора overline{a} - delim{|}{overline{a}}{|} .
— ?

Решение:
Определяем длину вектора delim{|}{overline{a}}{|} :
${delim{|}{overline{a}}{|}}=sqrt{{{a^2}_x}+{{a^2}_y}+{{a^2}_z}}=sqrt{{(-6^2)}+{10^2}+{(-2^2)}}=sqrt{140}.$

Ответ: {delim{|}{overline{a}}{|}}=sqrt{140}

Пример 14. Объем параллелепипеда

Дано:
Координаты векторов: overline{AB}=(-4,~4,~0);~overline{AC}=(-1,~3,~2);~overline{AD}=(-1,~-1,~1)

Найти:
Объем параллелепипеда ABCD.
V — ?

Решение:
Объем параллелепипеда ABCD вычисляется по формуле:
V=delim{|}{overline{AB}~overline{AC}~overline{AD}}{|}.

Найдём смешанное произведение векторов:
{overline{AB}~overline{AC}~overline{AD}}=delim{|}{matrix{3}{3}{{-4} {4} {0~} {-1} {3} {2~} {-1} {-1} {1~}}}{|}=-24

Объем параллелепипеда:
V=delim{|}{overline{AB}~overline{AC}~overline{AD}}{|}=delim{|}{-24}{|}=24.

Ответ: V=24.

Пример 15. Объем пирамиды

Дано:
Координаты векторов: overline{AB}=(-4,~4,~0);~overline{AC}=(-1,~3,~2);~overline{AD}=(-1,~-1,~1)

Найти:
Объем пирамиды ABCD.
V — ?

Решение:
Объем пирамиды ABCD вычисляется по формуле:
V={1/6}delim{|}{overline{AB}~overline{AC}~overline{AD}}{|}.

Найдём смешанное произведение векторов:
{overline{AB}~overline{AC}~overline{AD}}=delim{|}{matrix{3}{3}{{-4} {4} {0~} {-1} {3} {2~} {-1} {-1} {1~}}}{|}=-24

Вычисляем объём пирамиды:
V={1/6}delim{|}{overline{AB}~overline{AC}~overline{AD}}{|}={1/6}delim{|}{-24}{|}=4.

Ответ: V=4.

Аналитическая геометрия

Пример 16. Уравнение плоскости, проходящей через точку перпендикулярно вектору

Написать уравнение плоскости, проходящей через точку M₀ перпендикулярно вектору $overline{{M_1}{M_2}}$ .
Дано:
Координаты точек: M₀(2, 5, -3), M₁(7, 8, -1) и M₂(9, 7, 4).
Найти:
Уравнение плоскости, проходящей через точку M₀ перпендикулярно вектору $overline{{M_1}{M_2}}$ .

Решение:
В качестве нормального вектора плоскости vec{n} выбираем вектор $overline{{M_1}{M_2}}$ = {x₂-x₁, y₂-y₁, z₂-z₁} = {9-7, 7-8, 4-(-1)} = {2, -1, 5}.

Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) перпендикулярно вектору vec{n} = {A, B, C}, имеет вид A(x-x_0)+B(y-y_0)+C(z-z_0)=0 .

Составляем уравнение плоскости с нормальным вектором vec{n} = {2, -1, 5}, проходящей через точку M₀(2, 5, -3):
2(x-2)-1(y-5)+5(z+3)=0 .

Ответ: 2x-y+5z+16=0 .

Пример 17. Уравнение плоскости «в отрезках»

Какие отрезки отсекает на осях координат плоскость?
Дано:
Уравнение плоскости: 2x – 4y + 6z – 12 = 0.
Найти:
Отрезки, которые отсекает на осях координат плоскость.
a, b, c — ?

Решение:
Приведем общее уравнение плоскости {Ax}+{By}+{Cz}+D=0 к виду уравнения «в отрезках»:
{Ax}+{By}+{Cz}=-D,
Ax/{-D}+By/{-D}+Cz/{-D}=1,
x/{-D/A}+y/{-D/B}+z/{-D/C}=1.

Уравнение x/a+y/b+z/c=1 — это уравнение плоскости «в отрезках». Параметры a=-D/A,~b=-D/B,~c=-D/C,~ представляют собой координаты точек пересечения плоскости с координатными осями и равны (с точностью до знака) отрезкам, отсекаемым плоскостью на координатных осях.

Применяя вышеприведенное к уравнению 2x – 4y + 6z –12 = 0, получим:
{2x}/12-{4y}/12+{6z}/12=1~{doubleright}~{x/6}+{y/{-3}}+{z/2}=1 .

Отрезки, отсекаемые на осях, равны a = 6, b =−3, c = 2.
Отрицательный знак перед b показывает, что плоскость пересекает отрицательную полуось Oy.

Задачи по теме «Уравнение плоскости в пространстве»

Задача 1. Составить канонические уравнения прямой: $delim{lbrace}{matrix{2}{9}{{2x} {+} {y} {-} {5z} {-} {3} {=} {0~} {5x} {+} {3y} {+} {8z} {-} {13} {=} {0~} {x_3} {=} }}{}.$

Решение:
Для составления канонического или параметрического уравнения прямой в пространстве, нужно знать координаты какой-либо точки, лежащей на этой на этой прямой, и координаты вектора, коллинеарного прямой.
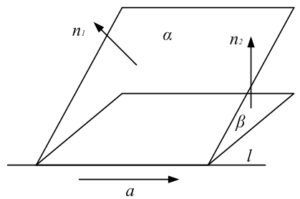
Рисунок к задаче №1
Так как прямая является линией пересечения двух плоскостей, ее направляющий вектор а параллелен каждой из этих плоскостей и соответственно перпендикулярен нормалям n₁ и n₂ к данным плоскостям. В таком случае он коллинеарен векторному произведению [n₁, n₂].
n₁ = (2; 1; -5), n₂ = (5; 3; 8), [n₁, n₂] = (23; -41; 1).
Итак, (l; m; n) = (23; -41; 1).

Найдем точку, лежащую на данной прямой, у которой одна из координат принимает выбранное нами значение; тогда остальные две координаты можно определить из системы уравнений, задающей пересекающиеся плоскости.

Примем для удобства вычислений z₀ = 0, тогда для точки A={х₀; у₀; 0}
$delim{lbrace}{matrix{2}{7}{{2x_0} {+} {y_0} {-} {3} {=} {0~} {5x_0} {+} {3y_0} {-} {13} {=} {0~} {x_3} {=} }}{}~doubleright$ $delim{lbrace}{matrix{2}{9}{{y_0} {=} {3} {-} {x_0} {~} {~} {~} {~} {5x_0} {+} {9} {-} {6x_0} {-} {13} {=} {0~}}}{}~doubleright$ x₀ = -4; y₀ = 11; A = {4; 11; 0}.

Cоставим канонические уравнения данной прямой:
{x+4}/23={y-11}/{-41}=z/1 .

Ответ: {x+4}/23={y-11}/{-41}=z/1 .

Задача 2. Составить уравнение плоскости, проходящей через прямую k:
delim{lbrace}{matrix{3}{3}{{x} {=} {2d-3~} {y} {=} {d+5~} {z} {=} {-d-1~} }}{} и точку B = {2; -3; 1}.

Решение:
Так как точка А = {-3,5,-1} принадлежит плоскости, значит вектор AB параллелен плоскости.
Так как данная прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости.
Значит, нормаль к плоскости коллинеарна векторному произведению этих векторов.

Так как прямая лежит в плоскости, ее направляющий вектор a = (2; 1; -1) параллелен плоскости. При d = 0 из уравнений прямой получаем:
delim{lbrace}{matrix{3}{3}{{x} {=} {-3~} {y} {=} {5~} {z} {=} {-1~} }}{} — координаты точки А, принадлежащей прямой и соответственно плоскости.
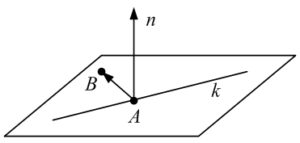
Рисунок к задаче №2

Получается, что вектор AB = (5; -8; 2) параллелен плоскости. Значит, нормаль n к плоскости коллинеарна векторному произведению [a, AB] = (-6; -9; -21).
Примем n = (2; 3; 7) и составим уравнение плоскости, проходящей через точку B перпендикулярно n:
2(x-2)+3(y+3)+7(z-1)=0,~2x+3y+7z-2=0.

Ответ: 2x + 3y + 7z – 2 = 0.

Задача 3.Написать уравнение плоскости, которая проходит через три точки с координатами N₁(x₁, y₁, z₁), N₂(x₂, y₂, z₂), N₃(x₃, y₃, z₃).

Решение:
Предположим, что какая нибудь, находящаяся на плоскости точка N, имеет координаты (x, y, z). Для этого случая уравнение плоскости примет вид:
(r-r₀, a, b) = 0,
где
r = (x, y, z);
r₀ = (x₁, y₁, z₁);
базисные векторы (смотрите рисунок) соответственно равны $a=vec{{N_1}{N_2}}$ и $b=vec{{N_1}{N_3}}$ .

Если записать смешанное произведение в виде определителя, то получим необходимое уравнение плоскости:
$delim{|}{matrix{3}{3}{{x-x_1} {y-y_1} {z-z_1~} {x_2-x_1} {y_2-y_1} {z_2-z_1~} {x_3-x_1} {y_3-y_1} {z_3-z_1~} }}{|}=0.$

Ответ: $delim{|}{matrix{3}{3}{{x-x_1} {y-y_1} {z-z_1~} {x_2-x_1} {y_2-y_1} {z_2-z_1~} {x_3-x_1} {y_3-y_1} {z_3-z_1~} }}{|}=0.$

Высшая математика

Решение примеров