Ряды

Формулы и уравнения рядов
• Числовые ряды
• Функциональные ряды
• Тригонометрические ряды. Ряд Фурье

Примеры решения рядов здесь.

Числовые ряды

Факториал и двойные факториалы:

— формула Стирлинга.

Геометрическая прогрессия:

|q|<1.

Основные определения и теоремы о рядах:

{u_n} — заданная бесконечная числовая последовательность,

— числовой ряд,
u_n — члены ряда,
– частичные суммы ряда.

Сумма ряда:

сходится, S — сумма ряда.

или ряд сходится и суммы нет.

Отбрасывание конечного числа членов ряда не влияет на его сходимость (но влияет на сумму).

Свойства сходящихся рядов:

Теоремы сравнения рядов с положительными членами:
≥ 0, ≥ 0.
1. ≤
   Если сходится, то сходится;
   если расходится, то расходится.
2. v_n ≠ 0, 0 < k < ∞.
   Либо и , и сходятся,
   либо и , и расходятся.

Достаточные признаки сходимости числовых рядов с положительными членами (u_n > 0)
• Признак Даламбера
  Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
• Признак Коши
  Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
• Интегральный признак сходимости
  1) u_n > 0; 2) u_n ≥ u_n+1; 3) f(x) — непрерывная невозрастающая функция, f(n) = u_n.
  Либо и , и сходятся,
  либо и , и расходятся.

Знакопеременные ряды
• Абсолютная сходимость
  Ряд сходится, откуда следует, что ряд сходится.
• Условная сходимость
  Ряд расходится, но ряд сходится.
• Знакочередующиеся ряды
  Ряды вида или где u_n > 0.
• Признак Лейбница (сходимости знакочередующегося ряда)
  Если 1) u₁ > u₂ > u₃ > …, 2) то 1) ряд сходится; 2) его сумма S > 0, и 3) S < u₁.

Примеры числовых рядов
1. : сходится, если a > 1; расходится, если a ≤ 1.
2. : сходится, если a < 1; расходится, если a ≥ 1.
3. : сходится.
4. : сходятся, |q| < 1; расходятся, |q| ≥ 1.
5. : сходится;
6. : сходится, если a > 1; расходится, если a ≤ 1.
7. 
8. : сходится условно.
9. : сходится абсолютно.
10. : сходится абсолютно.

Функциональные ряды

Функциональный ряд – сумма вида

При из функционального ряда получается числовой ряд

Если для числовой ряд сходится, то точка называется точкой сходимости функционального ряда. Если в каждой точке числовые ряды сходятся, то функциональный ряд называется сходящимся в области . Совокупность всех точек сходимости образует область сходимости функционального ряда.

– частичные суммы ряда. Функциональный ряд сходится к функции f(x), если

Равномерная сходимость

Функциональный ряд, сходящийся для всех из области сходимости, называется равномерно сходящимся в этой области, если ∀ε > 0 существует не зависящий от x номер N(ε), такой, что при n > N(ε) выполняется неравенство R_n(x) < ε для всех x из области сходимости, где — остаток ряда.

Геометрический смысл равномерной сходимости:

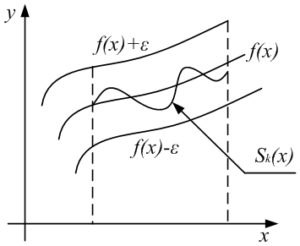
если окружить график функции y = f(x) «ε-полоской», определяемой соотношением f(x)−ε > y > f(x)+ε, то графики всех частичных сумм S_k(x), начиная с достаточно большого k, ∀x ∈ [a, b] целиком лежат в этой «ε-полоске», окружающей график предельной функции y = f(x).

— называется мажорируемым в области , если существует такой сходящийся числовой ряд u_n > 0, что для ∀x ∈ D f_n(x) ≤ u_n, n = 1, 2, …. Ряд называется мажорантой ряда

Признак Вейерштрасса (признак равномерной сходимости функционального ряда): функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

Степенные ряды:
— степенной ряд по степеням
При – степенной ряд по степеням x.

Область сходимости степенного ряда:
Радиус сходимости, интервал сходимости R, x ∈ (-R, R):
или
При |x| < R ряд сходится, при |x| > R – расходится;
в точках x = ±R – дополнительное исследование.

На интервале сходимости ряд сходится абсолютно;
на любом отрезке из интервала сходимости он сходится равномерно.

Свойства степенных рядов
1. Степенной ряд сходится равномерно на [−R′, R′]
   ∀R′ < R, его можно почленно дифференцировать и интегрировать в интервале сходимости.
2. 
3. Ряды, полученные почленным дифференцированием и интегрированием, имеют тот же интервал сходимости.

Разложение элементарных функций в степенные ряды

1. , x ∈ (−∞; ∞).
2. ,
   x ∈ (−∞; ∞).
3. , x ∈ (−∞; ∞).
4. , x ∈ (−∞; ∞).
5. , x ∈ (−∞; ∞).
6. 
   , x ∈ (−1; 1].
7. 
   , x ∈ [−1; 1).
8. ,
   x ∈ (−1; 1).
9. , x ∈ [−1; 1].
10. , x ∈ [−1; 1].
11. , x ∈ (−1; 1).
12. , x ∈ (−1; 1).
13. , x ∈ (−1; 1).
14. , x ∈ (−1; 1).
15. , x ∈ (−1; 1].

Тригонометрические ряды

Ряд Фурье для периодической функции с периодом 2π
• Ряд Фурье функции f(x):
  
• Коэффициенты Фурье:
  

Разложение в ряд Фурье четных и нечетных функций с периодом 2π
• f(-x) = f(x)
  ряд Фурье содержит только косинусы кратных дуг:
  
• f(-x) = -f(x)
  ряд Фурье содержит только синусы кратных дуг:
  

Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):

где

Разложение в ряд Фурье непериодических функций, заданных на отрезке x ∈ [0; l] или на отрезке x ∈ [-l; l]
Произвольная функция f(x) задана на отрезке [0; l]; на отрезок [-l; 0] она может быть продолжена произвольным образом:
– некоторая кусочно-монотонная функция.
Наиболее часто встречающиеся продолжения:
• f₁(x)=f(-x), x ∈ [-l; 0] (четное продолжение)
  
  где x ∈ [0; l] n = 0, 1, 2,…
• f₁(x) = —f(−x), x ∈ [-l; 0]
  (нечетное продолжение)
  
  где x ∈ [0; l] n = 1, 2,…
• На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть,
  – левый предел f(x) в точке x = l,
  – правый предел f(x) в точке x = l.